Introduction
If you’ve completed the earlier exercises on Refraction of Light at Plane Surfaces, Exercise 4(D) is where things get more challenging. This part of ICSE Class 10 Physics Selina Solutions Chapter 4 focuses on advanced numerical problems and application-based questions that require a strong grasp of concepts and formulas.
Why Exercise 4(D) is Important
This section combines everything you’ve learned so far laws of refraction, refractive index, and speed of light in different media into complex, exam-style problems. Many of these types of questions have appeared in past board exams, making this exercise a must-practice before your finals.
Benefits of Using Selina Solutions for Exercise 4(D)
- Clear Step-by-Step Methods – Each solution is explained logically so you can follow the reasoning.
- Exam-Oriented – Solutions match the ICSE Class 10 syllabus and marking scheme.
- Confidence Building – Helps you tackle high-difficulty questions without hesitation.
Exercise 4(D): (A) Multiple Choice Type
(Choose the correct answer from the options given below).
Question 1
At angle of incidence equal to the critical angle, the angle of refraction is:
(a) 0° (b) 30°
(c) 90° (d) 180°
Answer:
(c) 90°
Explanation:
The critical angle is defined as the angle of incidence in the denser medium for which the angle of refraction in the rarer medium is 90°.
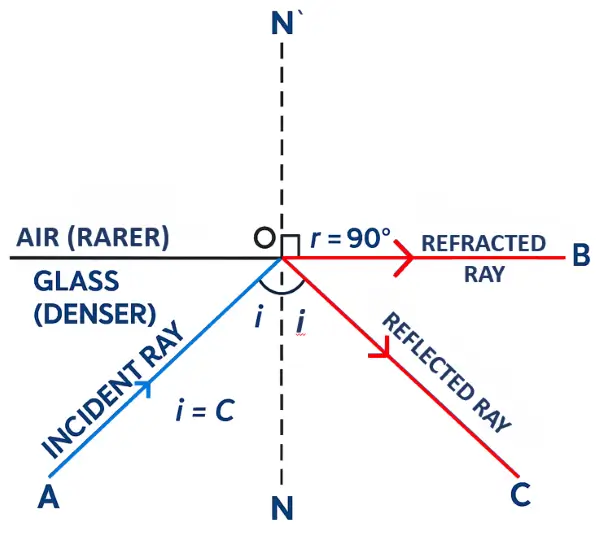
Question 2
The condition required for total internal reflection to take place is:
(a) light ray passes from a rarer to denser medium
(b) light ray passes from a denser to rarer medium
(c) angle of incidence is less than critical angle
(d) none of the above
Answer:
(b) light ray passes from a denser to rarer medium
Explanation:
Conditions for Total Internal Reflection (TIR):
(i) The light must travel from a denser medium to a rarer medium (e.g., from glass to air).
(ii) The angle of incidence must be greater than the critical angle for that pair of media.
Question 3
A scientist while performing an experiment desires that no incident light escapes from the top of a glass block. He varies the angle X continuously and finally manages to achieve his objective. Which of the following options describes the correct answer?
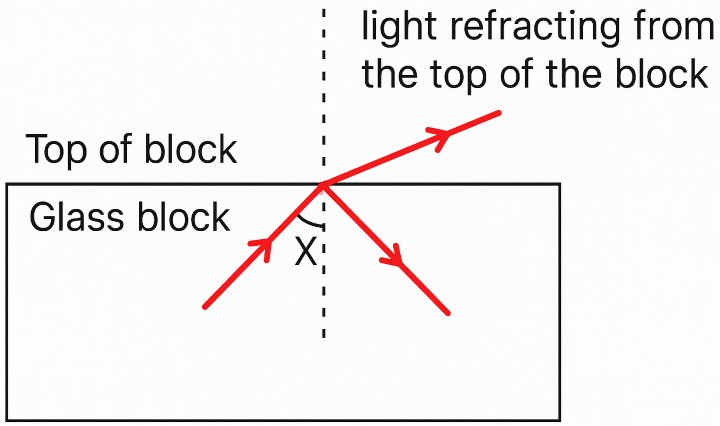
| Angle | Effect | |
| (a) | Decreased | Total Internal Reflection |
| (b) | Decreased | Total Internal Reflection |
| (c) | Increased | Total Internal Reflection |
| (d) | Increased | Total Internal Reflection |
Answer:
(d) Increased – Total Internal Reflection
Explanation:
By increasing the angle X, the angle of incidence becomes greater than the critical angle, so Total Internal Reflection happens.
This means all light reflects inside the glass
Question 4
When a ray of light travels from substance A to substance B and reaches their boundary, it suffers total internal reflection. Out of the following possibilities, which one is correct?
| Angle i | Substance B | |
| (a) | i < C | Optical density of A is less than B |
| (b) | i = C | Optical density of A is more than B |
| (c) | i > C | Optical density of A is less than B |
| (d) | i > C | Optical density of A is more than B |
Answer:
(d) i > C, Optical density of A is more than B
Explanation:
Total Internal Reflection (TIR) occurs when:
(i) Light travels from a denser medium (higher optical density) to a rarer medium (lower optical density).
(ii) The angle of incidence i is greater than the critical angle C.
Question 5
An equilateral prism can be used to deviate a ray of light through:
(a) 30° (b) 60°
(c) 75° (d) 90°
Answer:
(b) 60°
Explanation:
An equilateral prism has all angles equal to 60°, and when a light ray passes through it, it bends twice — once on entry and once on exit.
The angle of deviation (δ) is the angle between the direction of the incident ray and the emergent ray.
Question 6
Which of the following figures will depict deviation of ray of light A through 180°
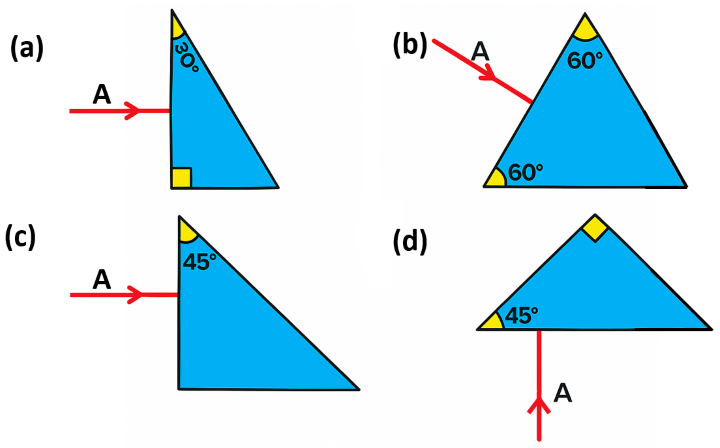
Answer:
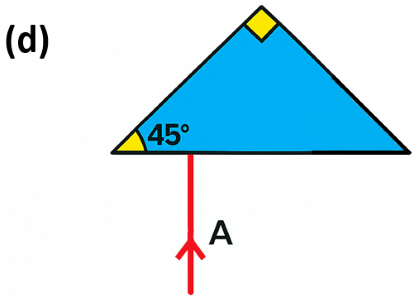
Explanation:
In Figure (4), the ray of light undergoes two reflections inside the isosceles right-angled prism, causing the ray to return back in the direction it came from, which is a 180° deviation.
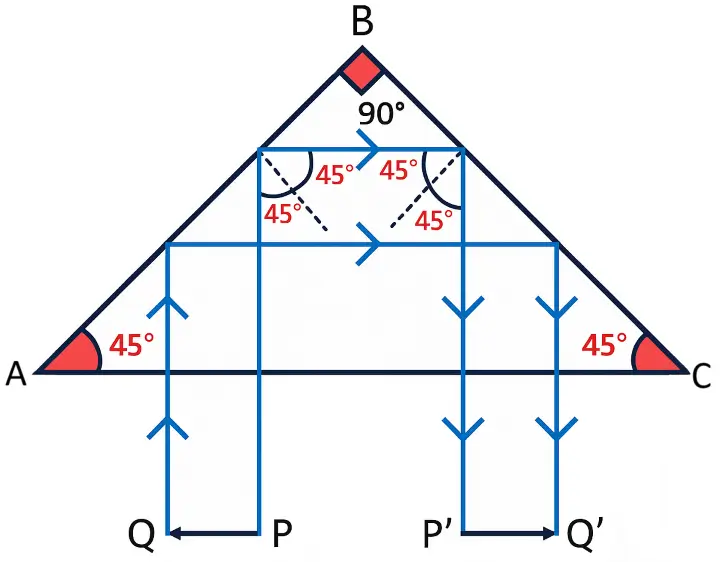
Question 7
The diagram below shows a light source P embedded in a rectangular glass block ABCD of critical angle 42°. The ray PQ would:
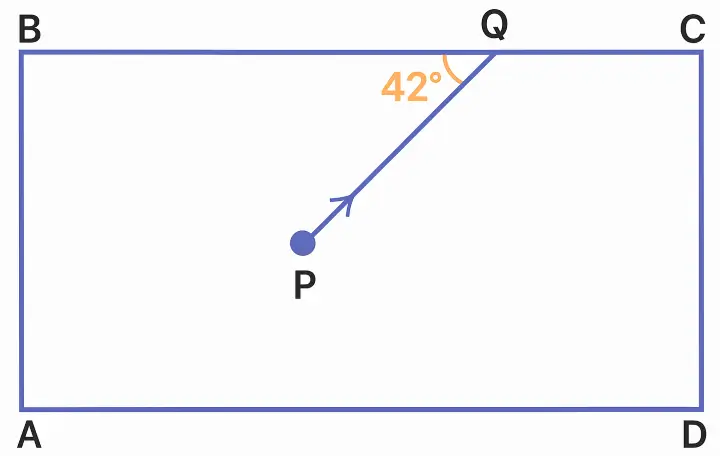
(a) pass undeviated
(b) suffer refraction
(c) suffer reflection
(d) suffer total internal reflection
Answer:
(d) suffer total internal reflection
Explanation:
The angle of incidence 48° is greater than the critical angle 42°, causing total internal reflection.
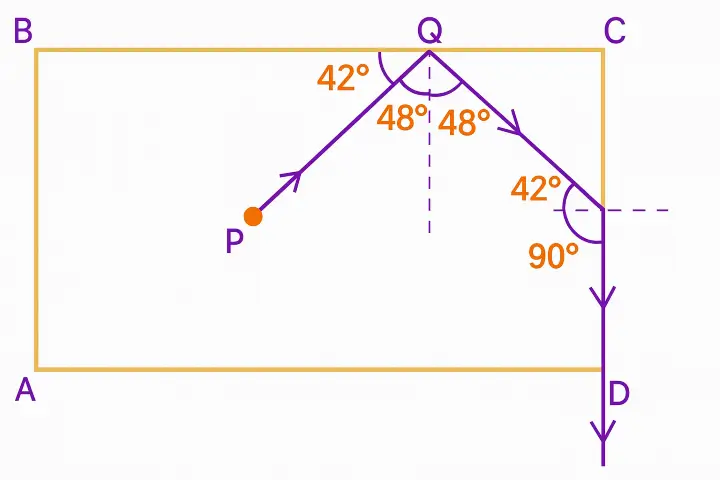
Question 8
In the process of total internal reflection, …………… of energy (or intensity) of light is reflected back.
(a) 70% (b) 80%
(c) 100% (d) 50%
Answer:
(c) 100%
Explanation:
During total internal reflection, the entire light wave is reflected back into the original medium without any loss of energy or intensity. As a result, 100% of the light’s energy is reflected.
Question 9
Out of violet, blue, yellow and red, the critical angle would be the least for …………… light for a pair of media.
(a) violet (b) blue
(c) blue (d) yellow
Answer:
(a) violet
Explanation:
The critical angle depends on the refractive index, and the refractive index of a material increases with decreasing wavelength (i.e., violet has the shortest wavelength and highest refractive index).
Exercise 4(D): (B) Very Short Questions
Question 1
How is the critical angle related to the refractive index of a medium?
Answer:
The critical angle is related to the refractive index by the relation: \({{}_a\mu}_g=\frac1{\sin\;C}\)
Question 2
State the approximate value of the critical angle for
(i) glass-air surface
(ii) water-air surface.
Answer:
(i) Refractive index, \({{}_a\mu}_g=\frac32\)
\({{}_a\mu}_g=\frac1{\sin\;C}\)
\(\Rightarrow\frac{3}{2}=\frac{1}{sin\ C}\)
\(\Rightarrow\ sin\ C=\frac{2}{3}\)
\(\Rightarrow\ C = 42°\)
Hence, critical angle for glass air surface is 42°.
(ii) Refractive index, \({{}_a\mu}_w=\frac43\)
\({{}_a\mu}_w=\frac1{\sin\;C}\)
\(\Rightarrow\frac{4}{3}=\frac{1}{sin\ C}\)
\(\Rightarrow\ sin\ C=\frac{3}{4}\)
\(\Rightarrow\ C = 49°\)
Hence, critical angle for glass air surface is 49°.
Question 3
A light ray is incident from a denser medium on the boundary separating it from a rarer medium at an angle of incidence equal to the critical angle. What is the angle of refraction for the ray?
Answer:
The angle of refraction is 90°.
Question 4
The critical angle for glass-air is 45° for the light of yellow colour. State whether it will be less than, equal to, or more than 45° for
(i) red light,
(ii) blue light ?
Answer:
(i) red light – More than 45° (since red light has a lower refractive index)
(ii) blue light – Less than 45° (since blue light has a higher refractive index)
Question 5
Which colour of light has higher critical angle? Red light or green light.
Answer:
Red light has a higher critical angle than green light because it has a lower refractive index.
Question 6
Fill in the blanks to complete the following sentences:-
(i) Total internal reflection occurs only when a ray of light passes from a …………… medium to a …………… medium.
(ii) Critical angle is the angle of …………… in denser medium for which the angle of …………… in rarer medium is ……………
Answer:
(i) Total internal reflection occurs only when a ray of light passes from a denser medium to a rarer medium.
(ii) Critical angle is the angle of incidence in denser medium for which the angle of refraction in rarer medium is 90°.
Question 7
State whether the following statement is true or false:
If the angle of incidence is greater than the critical angle, light is not refracted at all, when it falls on the surface from a denser medium to a rarer medium.
Answer:
True
This is the condition for total internal reflection.
Exercise 4(D): (C) Short Questions
Question 1
What is meant by the statement ‘the critical angle for diamond is 24°’?
Answer:
Critical angle for diamond is 24°, means that, when light travels from the diamond to air, the angle of incident is 24° for which the angle of refraction will be 90°.
Question 2
Name two factors which affect the critical angle for a given pair of media. State how do the factors affect it.
Answer:
The critical angle depends on two factors:
(i) The colour or wavelength of light : The refractive index of a transparent medium decreases with the increase of wavelength of light. (It is most for violet light and least for red light), therefore the critical angle for a pair of media is least for the violet light and most for the red light, i.e. the critical angle increases with the increase in wavelength of light.
(ii) The temperature : On increasing the temperature of medium, its refractive index decreases. So, the critical angle for the pair of medium increases with increase in temperature.
Question 3
The refractive index of air with respect to glass is expressed as gμa \(=\frac{\sin\;i}{\sin\;r}\)
(a) Write down a similar expression for aμg in terms of the angles i and r.
(b) If angle r = 90°, what is the corresponding angle i called?
(c) What is the physical significance of the angle i in part (b)?
Answer:
(i) The expression for aμg \(=\frac{\sin\;r}{\sin\;i}\)
(ii) When refractive angle r = 90° then, the corresponding angle of incidence i will be equal to critical angle.
(ii) Total internal reflection occurs, if the angle of incidence exceeds the value of i obtained in part (b)
Question 4
The table below gives refractive indices of some substances with respect to air.
| Substance | Refractive Index (μ) |
| Water | 1.33 |
| Turpentine | 1.47 |
| Glass | 1.58 |
| Diamond | 2.41 |
(a) Which medium will have the lowest critical angle and which will have highest critical angle with respect to air.
(b) If the temperature of all the substances is raised by C, what will happen to their critical angle?
Answer:
(a) Diamond has lowest critical angle and water has highest critical angle.
(b) If the temperature of all the substance is raised by C then the critical angle of the all the media will increase.
Question 5
Mention one difference between the reflection of light from a plane mirror and total internal reflection of light from a prism.
Answer:
| Plane mirror | Prism |
| In reflection of light from a plane mirror, only a part of the light is reflected while rest is refracted and absorbed. So, the reflection is partial. | In total internal reflection of light from a prism, the entire incident light is reflected back into the denser medium. So there is no loss of light energy. |
Question 6
State one advantage of using a total reflecting prism as a reflector in place of a plane mirror.
Answer:
A total reflecting prism gives the image much brighter and the brightness remains unchanged even after the long use, while the image is less bright and the brightness gradually decreases which is obtained by a plane mirror.
Exercise 4(D): (D) Long Questions
Question 1
Explain the term critical angle with the aid of a labelled diagram.
Answer:
The critical angle is the angle of incidence in a denser medium for which the angle of refraction in the rarer medium becomes 90°.

Question 2
(a) What is total internal reflection?
(b) State two conditions necessary for total internal reflection to occur.
(c) Draw diagram to illustrate total internal reflection.
Answer:
(a) When a ray of light travelling in a denser medium, is incident at the surface of a rarer medium at the angle of incidence greater than the critical angle for the pair of media, the ray is totally reflected back into the denser medium. This phenomenon is known as total internal reflection.
(b) The two necessary conditions for total internal reflection are —
(i) The light must travel from a denser medium to a rarer medium.
(ii) The angle of incidence must be greater than the critical angle for the pair of media.
(c) Below diagram illustrate total internal reflection:
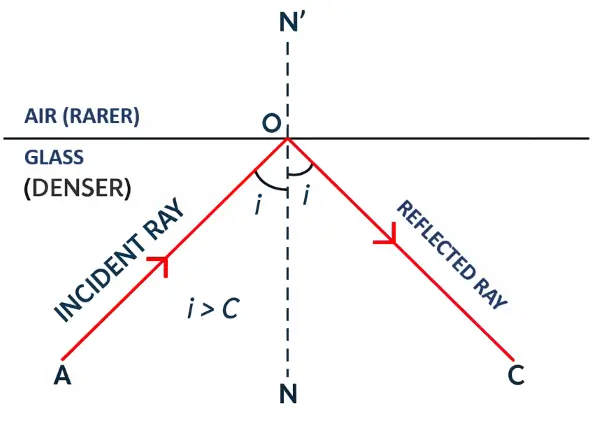
Question 3
Figure below shows two rays A and B travelling from water to air. If the critical angle for water-air surface is 48°, complete the ray diagram showing the refracted rays for each. State conditions when the ray will suffer total internal reflection.
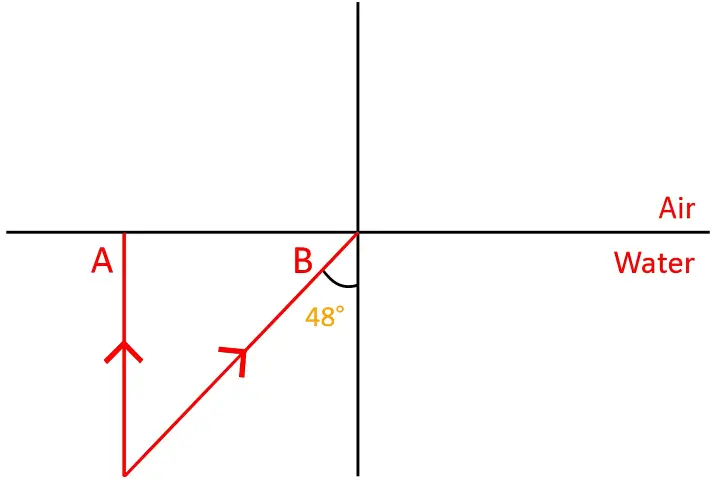
Answer:
Completed ray diagram with refracted rays labelled is shown below:
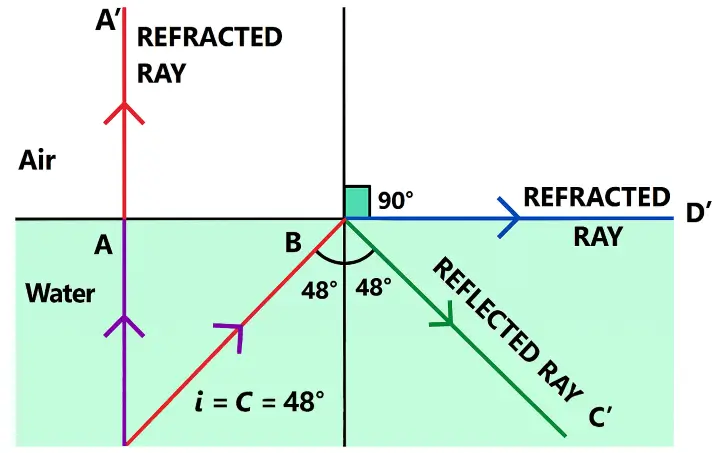
Conditions for Total Internal Reflection:
A ray will suffer total internal reflection if:
(i) It travels from a denser medium to a rarer medium (e.g., water to air).
(ii) The angle of incidence is greater than the critical angle ( i > 48° for water-air interface).
Question 4
Figure shows a point source P inside a water container. Three rays A, B and C starting from the source P are shown up to the water surface.
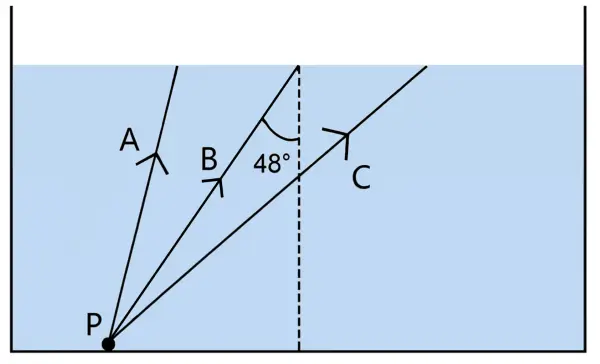
(a) Show in the diagram, the path of these rays after striking the water surface. The critical angle for water-air surface is 48°.
(b) Name the phenomenon which the rays A, B and C exhibit.
Answer:
(a) Below diagram shows the path of the rays after striking the water surface:
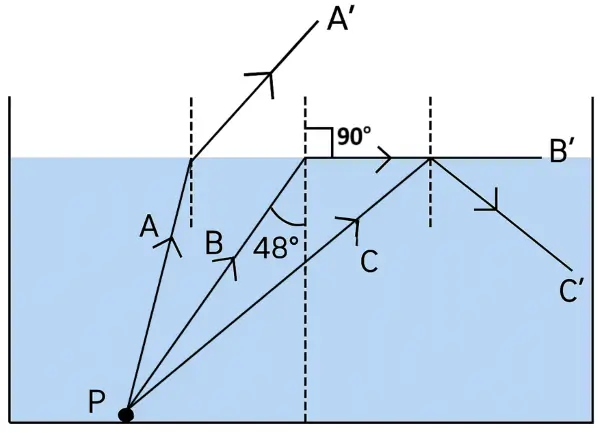
(b) Rays A and B show the phenomenon of ‘refraction of light’ and ray C shows the phenomenon of ‘total internal reflection’.
Question 5
In the figure, PQ and PR are the two light rays emerging from an object P. The ray PQ is refracted as QS.
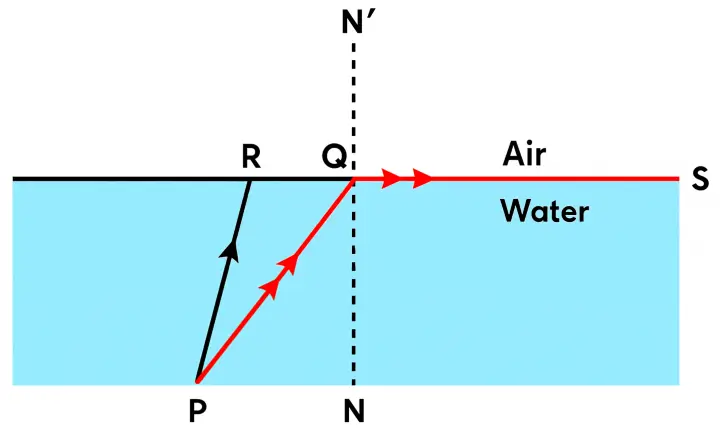
(a) State the special name given to the angle of incidence ∠PQN of the ray PQ.
(b) What is the angle of refraction for the refracted ray QS?
(c) Name the phenomenon that occurs if the angle of incidence ∠PQN is increased.
(d) The ray PR suffers partial reflection and refraction on the water-air surface. Give reason.
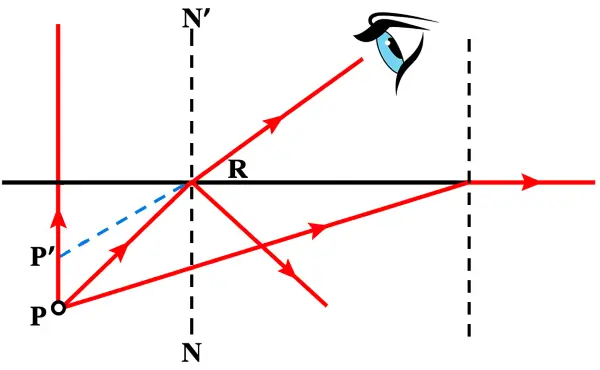
(e) Draw in the diagram the refracted ray for the incident ray PR and hence show the position of image of the object P by the letter P’ when seen vertically from above.
Answer:
(a) The angle of incidence ∠PQN is known as the critical angle.
(b) For the refracted ray QS, the angle of refraction is 90°.
(c) When the angle of incidence ∠PQN is increased, then the phenomenon that occurs is total internal reflection.
(d) For the ray PR, the angle of incidence is less than ∠PQN ( i.e the critical angle ). So according to the laws of reflection, ray PR suffers partial reflection and refraction.
(e) Below diagram shows the refracted ray and the position of image of the object P when seen vertically from above:
Question 6
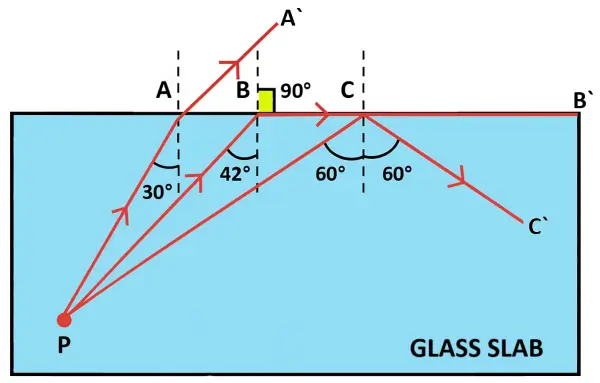
The refractive index of glass is 1.5. From a point P inside a glass slab, draw rays PA, PB and PC incident on the glass-air surface at an angle of incidence 30°, 42° and 60° respectively.
(a) In the diagram show the approximate direction of these rays as they emerge out of the slab.
(b) What is the angle of refraction for the ray PB? (Take sin 42° = 2/3)
Answer:
(a) Diagram with rays PA, PB and PC is shown below:
(b) Given,
Refractive index of glass, μ = 1.5
\(\mu=\frac{1}{sin\ C}\)
\(1.5=\frac{1}{sin\ C}\)
\(sin\ C=\frac{1}{1.5}=0.667\)
C = 41.8 ≈ 42°
Hence, the angle of incidence inside the glass block is 42°.
\(\frac{\sin\;i}{\sin\;r}={}_a\mu_g\)
\(\sin\;r={{}_a\mu}_g\times\sin\;i\)
\(\sin\;r={{}_a\mu}_g\times\sin\;42^\circ\)
Take sin 42° \(=\frac23\) and aμg \(=\frac32\)
\(\sin\;r=\frac32\times\frac23\)
\(\sin\;r=1\)
\(r=90^\circ\)
This shows that the ray PB is incident at the critical angle.
Question 7
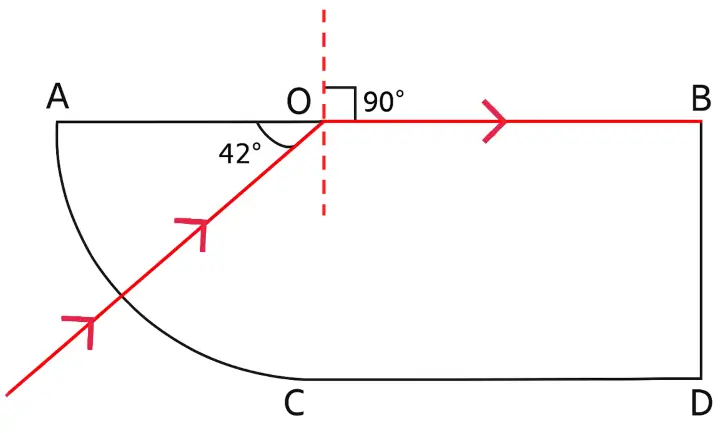
A ray of light enters a glass slab ABDC as shown in figure and strikes at the centre O of the circular part AC of the slab. The critical angle of glass is 42°. Complete the path of the ray till it emerges out from the slab. Mark the angles in the diagram wherever necessary.
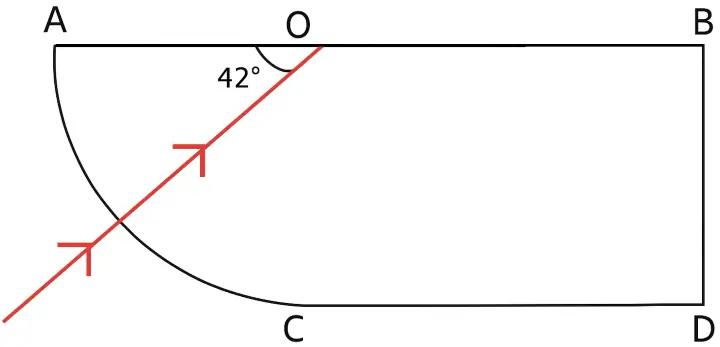
Answer:
Completed diagram showing the path of the ray till it emerges out from the slab is shown below:
Question 8
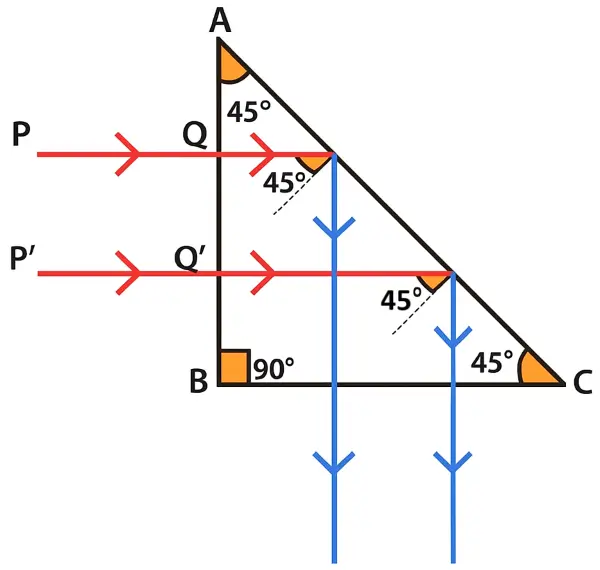
What is a total reflecting prism? State three actions that it can produce. Draw a diagram to show one such action of the total reflecting prism.
Answer:
A prism having an angle of 90° between its two refracting surfaces and the other two angles each equal to 45° is called a total reflecting prism. In such a prism, the light incident normally on any of its faces suffers total internal reflection inside the prism.
Due to this property, a total reflecting prism is used for the following three purposes :
- To deviate a ray of light through 90°.
- To deviate a ray of light through 180°.
- To erect the inverted image without producing deviation in its path.
Below diagram shows the deviation of a ray of light through 90° by a total reflecting prism:
Question 9
Show with the help of a diagram how a total reflecting prism can be used to turn a ray of light through 90°. Name one instrument in which such a prism is used.
Answer:

In the above figure, a beam of light is incident normally at the face AB. So, it passes undeviated into the prism and strikes at the face AC making an angle of incidence equal to 45°. Here the incidence is greater than the critical angle. So, the beam of light suffers total internal reflection and reflect at an angle of 45°. The reflected beam then strikes the face BC inside the prism where it is incident normally and thus passes undeviated. Hence, the incident beam gets deviated through 90°.
This type of prism is used in periscope.
Question 10
A ray of light XY passes through a right-angled isosceles prism as shown in the adjacent diagram.
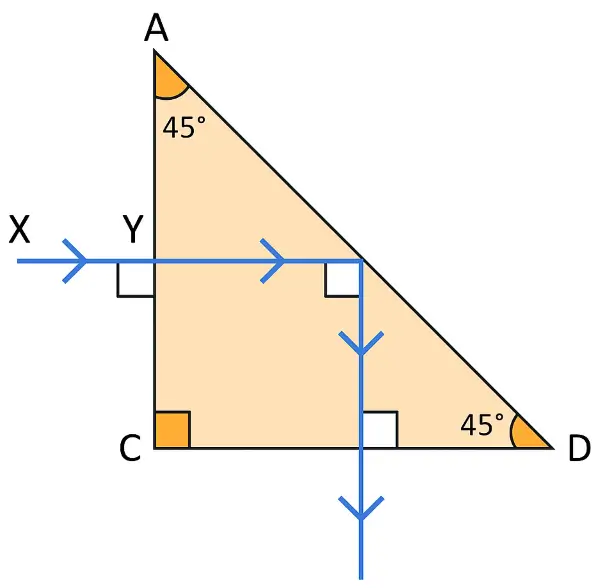
(a) What is the angle through which the incident ray deviates and emerges out of the prism?
(b) Name the instrument where this action of prism is put into use.
(c) Which prism surface will behave as a mirror?
Answer:
(a) Direction of the ray is perpendicular to the initial direction, the total deviation = 90°
(b) The instrument where this action of prism is put into use is the periscope.
(c) Surface AB acts like a mirror due to Total Internal Reflection.
Question 11
Draw a diagram of a right angled isosceles prism which is used to make an inverted image erect.
Answer:
A right-angled isosceles prism (with angles 90°, 45°, 45°) is often used to invert and erect images.
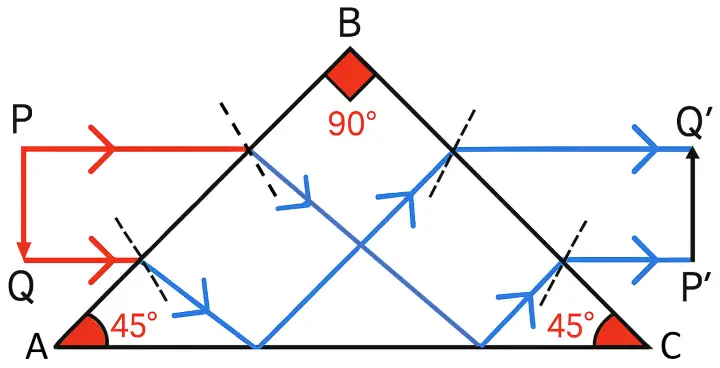
Device where it’s used: Periscope.
Question 12
In the figure, a ray of light PQ is incident normally on the hypotenuse of an isosceles right angled prism ABC.
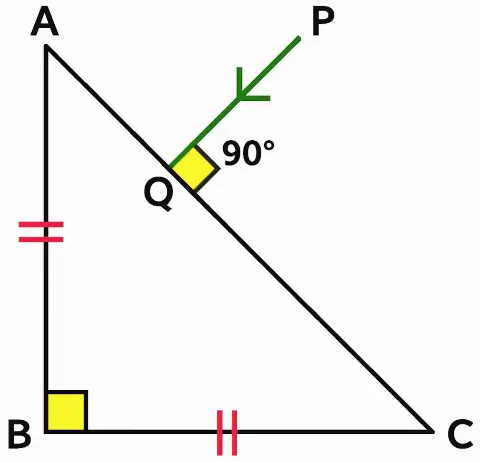
(a) Complete the path of the ray PQ till it emerges from the prism. Mark in the diagram the angle wherever necessary.
(b) What is the angle of deviation of the ray PQ?
(c) Name a device in which this action is used.
Answer:
(a) Below diagram shows the path of the ray PQ till it emerges from the prism with all the angles labelled:
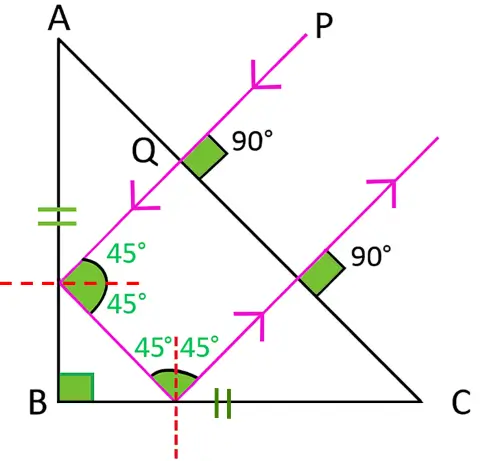
(b) The angle of deviation of the ray PQ is 180°.
(c) This action of the prism is used in Binoculars.
Question 13
In the figure given below, a ray of light PQ is incident normally on the face AB of an equilateral glass prism. Complete the ray diagram showing its emergence into air after passing through the prism. Take critical angle for glass = 42°.
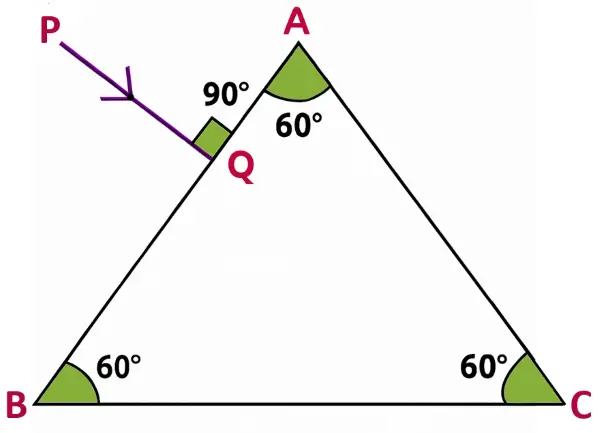
(a) Write the angles of incidence at the faces AB and AC of the prism.
(b) Name the phenomenon which the ray of light suffers at the face AB, AC and BC of the prism.
Answer:
(a)
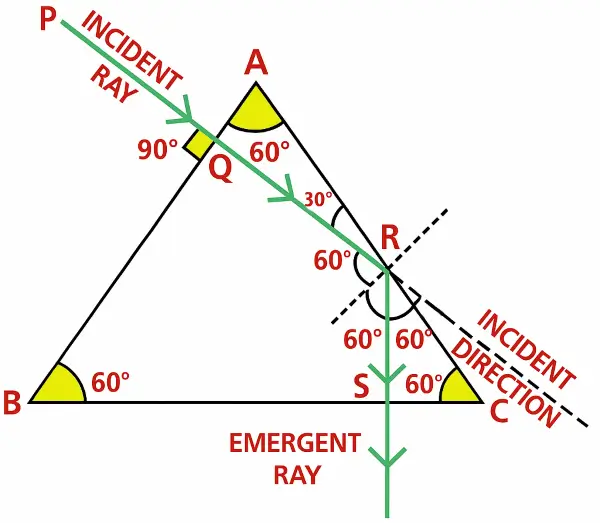
The angle of incidence at the faces AB, i = 0°.
The angle of incidence at the faces AC, i = 60°.
(b) The phenomenon which the ray of light suffers at:
face AB : refraction
face AC : total internal reflection
face BC : refraction
Question 14
Draw a neat labelled ray diagram to show total internal reflection of a ray of light incident normally on one face of a 30°, 90°, 60° prism.
Answer:
The diagram below shows a labelled ray diagram illustrating total internal reflection of a light ray incident normally on one face of a 30°, 60° and 90° prism.
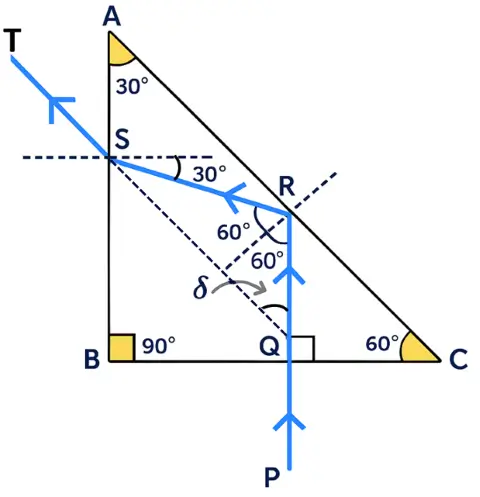
Question 15
Copy the diagram given below and complete the path of the light ray till it emerges out of the prism. The critical angle of glass is 42°. In your diagram mark the angles wherever necessary.
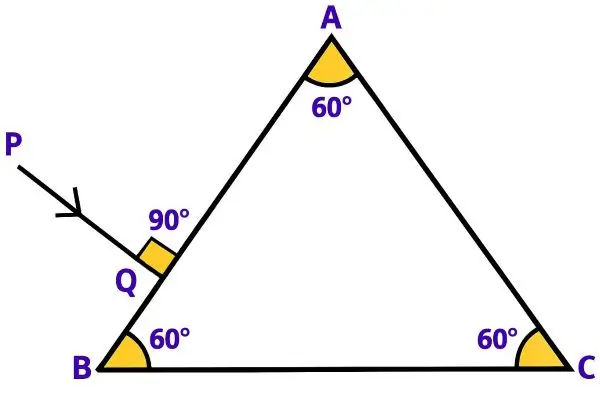
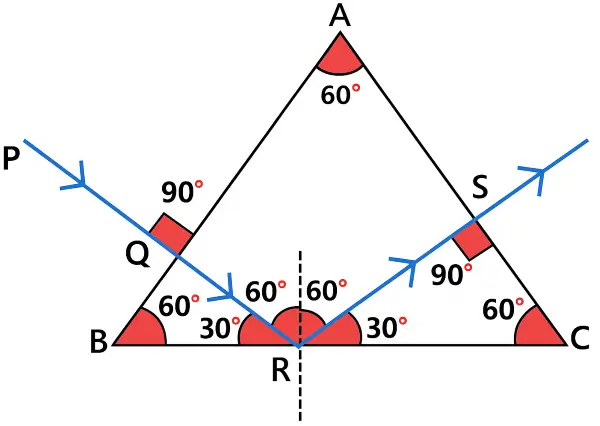
Answer:
Below is the completed diagram showing the path of the light ray till it emerges out of the prism with all angles marked:
Question 16
What device other than a plane mirror, can be used to turn a ray of light through 180°? Draw a diagram in support of your answer. Name an instrument in which this device is used.
Answer:
A total reflecting prism is used to turn a ray of light through 180°.

This device is used in a binocular and camera to invert the image without the loss of intensity.
Question 17
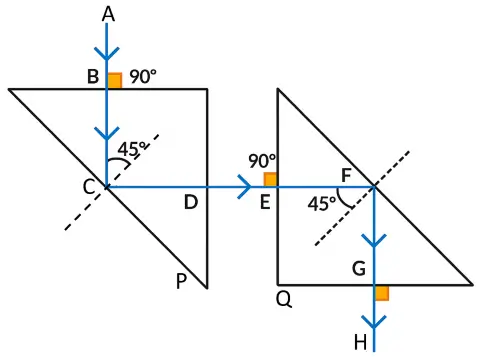
Two isosceles right-angled glass prisms P and Q are placed near each other as shown in figure. Complete the path of the light ray entering the prism P till it emerges out of the prism Q.
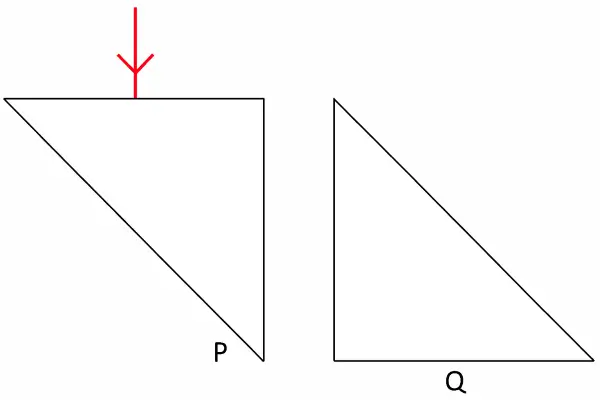
Answer:
The diagram below shows the path of a light ray as it enters the prism at point P and emerges from the prism at point Q.
Question 18
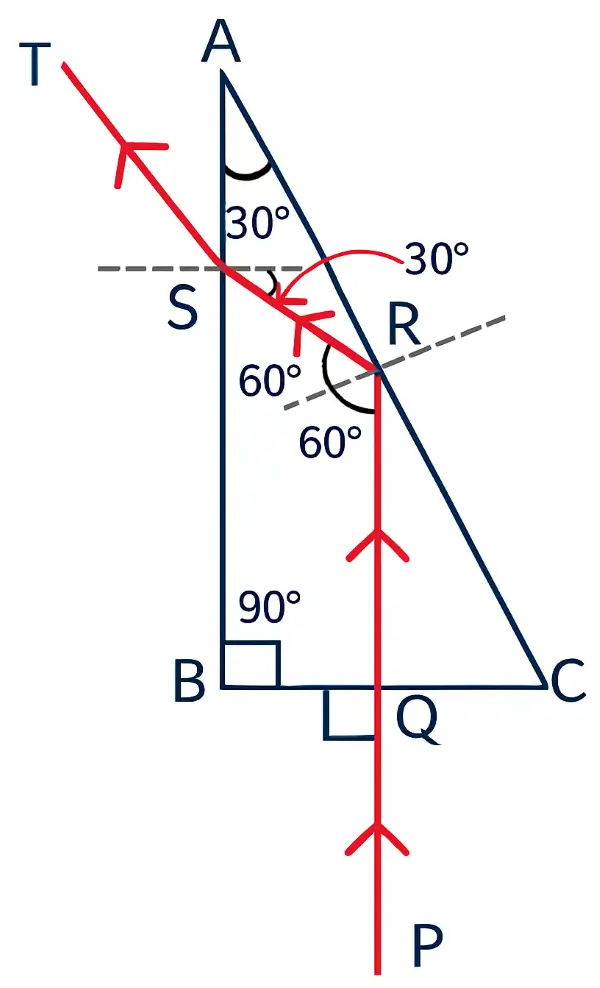
Complete the path of ray PQ through the glass prism ABC as shown in figure till it emerges out of the prism. Given the critical angle of glass is 42°.
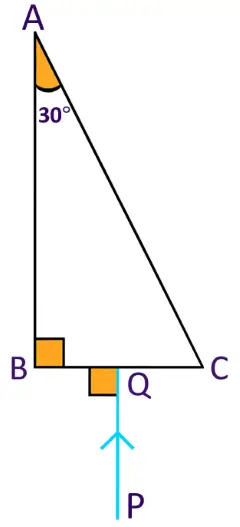
Answer:
The diagram illustrates the path of ray PQ as it travels through the glass prism ABC until it emerges from the prism.
Question 19
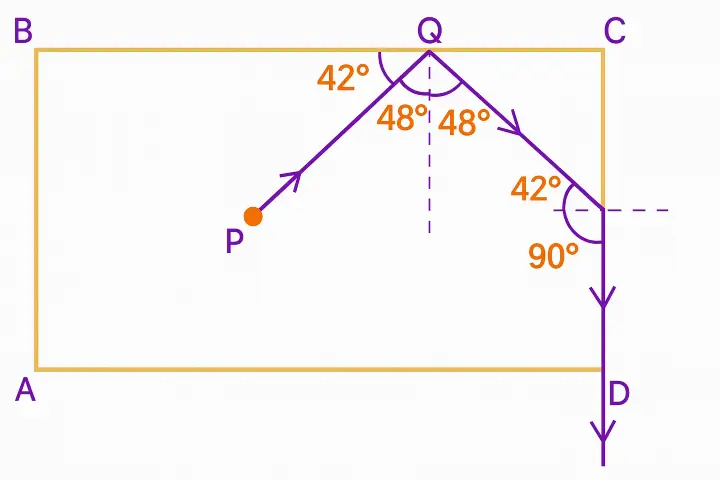
The diagram below shows a light source P embedded in a rectangular glass block ABCD of critical angle 42°. Complete the path of ray PQ till it emerges out of the block. [Write necessary angles]
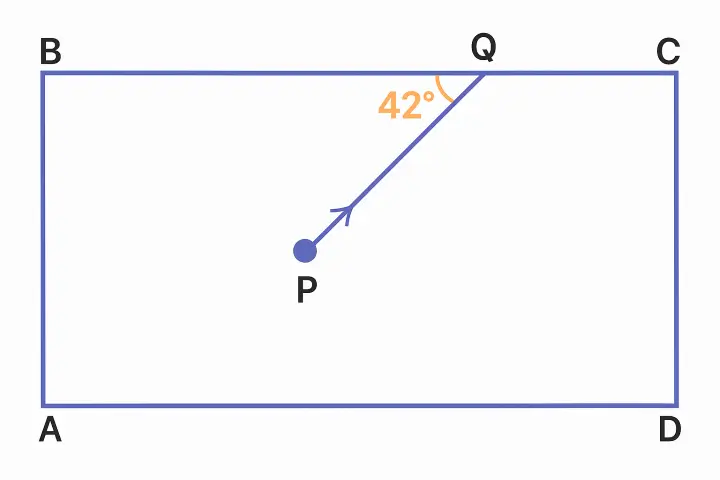
Answer:
Completed diagram showing the path of the ray PQ till it emerges out of the block is shown below:
Download Free Selina Concise Physics Class 10 Refraction of Light at Plane Surfaces Solutions
You can download free PDF solutions for Selina Class 10 Physics Exercise 4(A) to revise offline. These solutions are exam-ready and designed by subject experts.
Tips for Scoring in Exercise 4(D)
- Revise the formulas for refractive index and related speed of light equations.
- Always write down the given data and formula before solving.
- Check your unit conversions carefully to avoid mistakes.
- Use diagrams where applicable to make your answers more complete.

