ICSE Class 10 Physics Chapter 4 Notes

Introduction

Refraction of light is one of the most important topics in ICSE Class 10 Physics, and it often carries a good weightage in the board exam. This chapter, Refraction of Light at Plane Surfaces, explains how light bends when it passes from one medium to another and covers concepts like refractive index, apparent depth, and lateral shift.

Rohit Academy offers expert-curated ICSE Class 10 Physics Study Materials including ICSE Refraction of Light at Plane Surfaces Chapter Notes, diagrams, and key formulas for better understanding.

If you are preparing from the Selina ICSE Physics Class 10 textbook, this article will help you revise important definitions, formulas, and solved examples in a simple way.

Study materials related to chapter 4

Class 10 Chapter 4 Refraction of Light at Plane Surfaces Ex 4(A) Solutions

Class 10 Chapter 4 Refraction of Light at Plane Surfaces Ex 4(B) Solutions

Class 10 Chapter 4 Refraction of Light at Plane Surfaces Ex 4(C) Solutions

Class 10 Chapter 4 Refraction of Light at Plane Surfaces Ex 4(D) Solutions

Class 10 Chapter 4 – Refraction of Light at Plane Surfaces Previous Year Questions

SECTION A : REFRACTION ,  LAWS OF REFRACTION  AND  REFRACTIVE INDEX

When light falls on a surface , three things happen:

• Absorption
• Reflection
• Refraction

REFLECTION  OF  LIGHT

The phenomenon of bouncing back of light into the same medium after strike to the smooth surface is called reflection.

Laws of reflection

There are two laws of reflection:-

1. The angle of incidence is equal to the angle of reflection. 
   Angle of incidence = Angle of reflection [∠i = ∠r]
2. The incident ray, the normal ray and the reflected ray, all lie in the same plane.

MEDIUM

A transparent substance in which light travels is known as a medium. Medium can be divided into two types:

• Optically rarer medium:  A medium in which the speed of light is more is known as optically rarer medium (or less dense medium). Air is an optically rarer medium as compared to glass and water.

• Optically denser medium: A medium in which the speed of light is less, is known as optically denser medium. Glass is an optically denser medium than air and water.

Speed of light in some medium

• Speed of light in air (C) \(=\ 3\times{10}^8\ m\ s^{-1}\)
• Speed of light in water (V_w) \(=\ 2.25\times{10}^8\ m\ s^{-1}\)
• Speed of light in glass (V_g) \(=\ 2\times{10}^8\ m\ s^{-1}\)
• Speed of light in Diamond \(=\ 1.25\times{10}^8\ m\ s^{-1}\)

Refraction of light

• The change in the direction of the path of light, when it passes from one transparent medium to another transparent medium, is called refraction of light.
• The intensity of the refracted light is always less than that of the incident light because a portion of the incident light is reflected at the boundary.

• Incident ray : It is incoming ray on the refracting surface.
• Refracted ray : It is an outgoing ray from the refracting  surface.
• Angle of incidence (i) : It is the angle between incident rays and perpendicular line (normal) at the point of incidence.
• Angle of refraction (r) : It is the angle between refracted rays and perpendicular line (normal) at the point of incidence.

RULES OF REFRACTION

Rule 1 :

• When a light ray travels from a rarer medium to a denser medium, the light  ray  bends towards the normal. ( Trick : RDTN)

• Therefore, the angle of incidence (i) is greater than the angle of refraction (r). Hence, i > r.

• Angle of deviation, \(\delta=i-r\)

Rule 2 :

• When a light ray travels from a denser medium to a rarer medium, the light ray bends away from the normal. (Trick : DRAN)

• Therefore, the angle of incidence (i) is less than the angle of refraction (r). Hence, i < r.
• Angle of deviation, \(\delta=r-i\)

Rule 3 :

• When the light ray incident normally to the interface of two medium then it travels in same path , no deviation will be there.

• Thus, if angle of incidence ∠i = 0°, then the angle of refraction ∠r = 0°.

• Also, the angle of deviation of the ray will be 0⁰.

Cause of Refraction

• Refraction of light occurs because of this change in the speed of light due to a change in the medium.

• When ray of light  passes from an optically rarer medium to an optically denser medium, the speed of light decreases and light bends towards the normal. 

• When ray of light  passes from an optically denser medium to an optically rarer medium, the speed of light increases and light bends away from  the normal.

***Note

• Speed of light changes in the other medium due to its different optical density, even though the ray does not bend.

LAWS OF REFRACTION OF LIGHT (Snell’s Law)

The Snell’s laws of refraction of light are:

1. The incident ray, the refracted ray and the normal at the point of incidence, all lie in the same plane.
2. The ratio of sine of angle of incidence to the sine of angle of refraction is constant for a given pair of media.

\(\frac{sine\;of\;angle\;of\;incidence}{sine\;of\;angle\;of\;refraction}=cons\tan t\;={{}_1\mu}_2\)

\(\frac{sin\;i}{sin\;r}=cons\tan t\;={{}_1\mu}_2\)

This constant value is called the refractive index of the second medium with respect to the first.

REFRACTIVE INDEX

Refractive index is defined as the ratio of speed of light in medium 1 to the speed of light in medium 2. It is represented by μ (mew).

\({{}_1\mu}_2=\ \frac{Speed\ of\ light\ in\ medium\ 1}{Speed\ of\ light\ in\ medium\ 2}\)

It is read as refractive index of medium 2 with respect to medium 1.

There are two types of refractive index:

(i) Absolute refractive index : The refractive index of medium is defined as the ratio of the speed of light in vacuum (or air)  to the speed of light in that medium.

\(\mu_m=\ \frac{Speed\ of\ light\ in\ air\ (or\ vacuum)}{Speed\ of\ light\ in\ medium}=\ \frac{c}{v}\)

Absolute refractive index of some common substance

Substance (or Medium)	Refractive index (μ)
Vacuum / Air (Lowest)	1.00
Ice	1.31
Water	1.33
Alcohol	1.37
Glass	1.5
Ruby	1.76
Diamond (Highest)	2.41

***Note

• The refractive index of diamond is 2.41. It means that light travels in air 2.41 times faster than in diamond.
• Or, It means that the speed of light in diamond is 2.42 times slower than its speed in vacuum or air.

• Lower Refractive Index (e.g., air):
  Speed of light is faster
  Light bends less (less deviation)

• Higher Refractive Index (e.g., glass, diamond):
  Speed of light is slower
  Light bends more (more deviation)

• The absolute refractive index of a transparent medium is always greater than 1.

• There is no unit of the refractive index.

(ii) Relative refractive index : When light is going from one medium (other than vacuum or air) to another medium, then the value of refractive index is called relative refractive index.

\({{}_1\mu}_2=\ \frac{Speed\ of\ light\ in\ medium\ 1}{Speed\ of\ light\ in\ medium\ 2}=\ \frac{v_1}{v_2}\)

¹μ₂  means refractive index of medium 2 with respect to medium 1. That means, light travels from medium 1 to 2.

Example 

• Refractive Index of glass w.r.t water is (light travels from water to glass),
  \({{}^{water}\mu}_{glass}=\frac{Speed\;of\;light\;in\;water}{Speed\;of\;light\;in\;glass}\)
• Refractive Index of water w.r.t glass is (light travels from glass to water), 
  \({{}^{glass}\mu}_{water}=\frac{Speed\;of\;light\;in\;glass}{Speed\;of\;light\;in\;water}\)

Conditions for a light ray to pass undeviated on refraction

Refraction will not take place under the following two conditions:

1. If the incident ray falls normally (or perpendicularly) to the surface of a glass slab, then there is no bending of the ray of light, and it goes straight.
2. When the refractive indices of two media are equal.

Factors affecting the refractive index of a medium

(i) Nature of the medium:

•  Rarer medium → Faster speed of light → Lower refractive index
• Denser medium → Slower speed of light → Higher refractive index

(ii) Temperature: As temperature increases, the speed of light in the medium generally increases, so the refractive index decreases.

(iii) Wavelength of light:

• The speed of light of all the colours is the same in air (or vacuum), but in any other transparent medium, the speed of light is different for different colours.

• In a given medium, the speed of red light is maximum and that of the violet light is least.

• Violet light deviates the most, Red light deviates the least

• The refractive index of a transparent medium is maximum for violet light and least for red light.  

Wavelength: It is the distance between two successive crests or troughs of a wave.

***Note

\(Wavelength \propto Velocity \propto temperature \propto \frac{1}{Refractive\ Index}\)

Relationship between speed (V), frequency  and wavelength  of light

• Wavelength, \(\lambda=\frac Vf\)

• When light passes from a rarer to a denser medium, its wavelength decreases as the speed of light decreases.

• When light passes from a denser  to a rarer medium, its wavelength increases as the speed of light increases.
• Frequency (f)  remains unchanged.

***Note

• \(Wavelength \propto Velocity \propto \frac{1}{Refractive\ Index}\)

• Red Light → Maximum Wavelength → Maximum Velocity → Least Bending → Lowest Refractive Index

• Violet Light → Minimum Wavelength → Minimum Velocity → most Bending → Highest Refractive Index

Relationship between wavelength in the two medium

\(f=\frac C\lambda\) ……………(i)

\(f=\frac V{\lambda’}\) ……………(ii)

\(\frac C\lambda=\frac V{\lambda’}\)

\(\lambda’=\frac VC\lambda\)

\(\lambda’=\frac\lambda\mu\)                 

Where.
𝑓 = 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑙𝑖𝑔ℎ𝑡
𝑐 = 𝑠𝑝𝑝𝑒𝑑 𝑜𝑓 𝑙𝑖𝑔ℎ𝑡 𝑖𝑛 𝑎𝑖𝑟
𝑉 = 𝑠𝑝𝑝𝑒𝑑 𝑜𝑓 𝑙𝑖𝑔ℎ𝑡 𝑖𝑛 𝑚𝑒𝑑𝑖𝑢𝑚
𝜆 = 𝑤𝑎𝑣𝑒𝑙𝑒𝑛𝑔𝑡ℎ 𝑜𝑓 𝑙𝑖𝑔ℎ𝑡 𝑖𝑛 𝑎𝑖𝑟 

Principle of Reversibility 

According to principle of reversibility the path of light is reversible.

Proof:

According to Snell’s law,

₁μ₂ \(=\frac{\sin\;i}{\sin\;r}\)

₂μ₁ \(=\frac{\sin\;r}{\sin\;i}\)

₂μ₁ \(=\frac1{\frac{\sin\;i}{\sin\;r}}\)

\({{}_2\mu}_1=\frac1{{{}_1\mu}_2}\)

\({{}_1\mu}_2\;\times\;{{}_2\mu}_1=1\)

Example 
In the diagram below, the principle of reversibility is applied.

REFRACTION OF LIGHT THROUGH  A RECTANGULAR GLASS BLOCK

• On passing through a rectangular glass slab, a ray of light suffers two refractions, one while going from air to glass and the other while going from glass to air.

• Light emerges from rectangular slab in a direction parallel to that in which it entered the glass slab. However the final emergent ray is slightly shifted sideways from the direction of original incident ray by a distance x called lateral shift. 

• Incident ray and emergent rays are parallel to each other.

• The perpendicular distance between the incident ray and the emergent ray is called lateral displacement.

• Lateral displacement depends mainly on three factors:
  (i) Angle of incidence
  (ii) Thickness of glass block
  (ii) Refractive index of glass block

• Lateral displacement is directly proportional to
  (i) Angle of incidence
  (ii) Thickness of glass slab
  (iii) Refractive index of glass slab.

• Higher the values of these factors, greater will be the lateral displacement.

• The angle which the emergent ray makes with the normal is called the angle of emergence.

• Angle of incidence, ∠i = Angle of emergence, ∠e

Multiple images in a thick plane glass plate or thick mirror

• If an object is placed in front of a plane glass mirror of adequate thickness and is viewed obliquely, a number of images are seen.

• The second image is the brightest, while rest are of decreasing brightness.

• This image is the brightest image because it is due to the light suffering a strong reflection at the silver surface.

SECTION B : REFRACTION OF LIGHT THROUGH A PRISM

PRISM

• A transparent refracting medium which is bounded by five plane surfaces and having a triangular cross section is known as prism.

• Two opposite surfaces of the prism are identical parallel triangles, while the other three surfaces are rectangular and inclined on each other.

• The two rectangular plane inclined surfaces through which the light passes are called  refracting surfaces. 

• The third rectangular plane surface is the base of the prism.

• The angle between the two refracting surfaces is called the angle of prism.

Refraction of light through a glass prism

• PQRS is pathway of light through prism.

Different  Rays:

• Ray PQ → Incident ray on surface AB
• Ray QR → Refracted ray between surface AB and BC
• Ray RS → Emergent ray at surface AC
• N₁N & N₂N → Normal at point of incidence and emergence

Different  Angles:

• ∠𝐴 → 𝐴𝑛𝑔𝑙𝑒 𝑜𝑓 𝑝𝑟𝑖𝑠𝑚
•  ∠𝑖₁ → 𝐴𝑛𝑔𝑙𝑒 𝑜𝑓 𝑖𝑛𝑐𝑖𝑑𝑒𝑛𝑐𝑒 𝑎𝑡 𝑠𝑢𝑟𝑓𝑎𝑐𝑒 𝐴𝐵
•  ∠i₂ = ∠e → Angle of incidence (angle of emergence) at surface AC
•  ∠ 𝑟₁ → 𝐴𝑛𝑔𝑙𝑒 𝑜𝑓 𝑟𝑒𝑓𝑟𝑎𝑐𝑡𝑖𝑜𝑛 𝑎𝑡 𝑠𝑢𝑟𝑓𝑎𝑐𝑒 𝐴𝐵
•  ∠ 𝑟₂ → 𝐴𝑛𝑔𝑙𝑒 𝑜𝑓 𝑟𝑒𝑓𝑟𝑎𝑐𝑡𝑖𝑜𝑛 𝑎𝑡 𝑠𝑢𝑟𝑓𝑎𝑐𝑒 𝐴𝐶
•  ∠ 𝛿 → 𝐴𝑛𝑔𝑙𝑒 𝑜𝑓 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛
•  𝛿 = 𝛿₁ + 𝛿₂
• Angle of incidence (i₁) = Angle of emergence (i₂)
• Angle of Deviation: The angle between incident ray and emergent ray is called angle of deviation. 
• 𝑨 = 𝒓_𝟏 + 𝒓_𝟐
•  𝛿₁ = 𝑖₁ − 𝑟₁
•  𝛿₂ = 𝑖₂ − 𝑟₂
•  𝛿 = 𝛿₁ + 𝛿₂
•  𝛿 = (𝑖₁ − 𝑟₁) + (𝑖₂ − 𝑟₂)
•  𝛿 = (𝑖₁ + 𝑖₂) − (𝑟₁ + 𝑟₂)
•  𝛿 = (𝑖₁ + 𝑖₂) − 𝐴
•  𝜹 = (𝒊 + 𝒆) − 𝑨

***Note

• When light passes through a prism, it bends twice — once at the first surface (air to prism) and again at the second surface (prism to air).
  It always bends towards the base of the prism at both surfaces.
• If a ray of light is incident normally (perpendicularly) on a surface, then the angle of incidence is 0°.

Factors affecting the angle of deviation

The value of the angle of deviation depends on the following four factors:

(i) The angle of incidence (i) (𝒊 − 𝜹 𝒈𝒓𝒂𝒑𝒉)

• If the angle of incidence increases the angle of deviation decreases becomes minimum (𝛿_𝑚𝑖𝑛)  and then increases.

• When angle of deviation is minimum, the prism is said to be placed in the minimum deviation position.

• Angle of deviation becomes minimum (𝛿_𝑚𝑖𝑛) when the angle of incidence is equal to the angle of emergence (𝑖₁ = 𝑖₂ 𝑜𝑟 𝑟₁ = 𝑟₂).
  𝑤ℎ𝑒𝑛 𝛿 = 𝛿_𝑚𝑖𝑛 , 𝑖1 = 𝑖2 = 𝑖
  𝜹_𝒎𝒊𝒏 = 𝟐𝒊 − 𝑨

• In position of minimum deviation, the refracted ray inside the prism is parallel to its base.

(ii) On refractive index, μ: The prism with a higher refractive index produces a greater deviation.

(iii) The angle of prism (A) : Angle of deviation  increases with the increase in the angle of prism (A).

(iv) The colour or wavelength (λ) of light used : Angle of deviation decreases with the increase in the wavelength of light.
Thus the refractive index of the material of a prism for visible light is maximum for the violet colour and minimum for the red colour. Hence, a given prism deviates the violet the most and the red light least.

***Note

\(Deviation\;(\delta)\;\propto Refractive\;Index\;(\mu)\;\propto\;Angle\;of\;prism\;(A)\;\propto\;\frac1{wavelength\;\;of\;\;light\;(\lambda)}\)

SECTION C : SIMPLE APPLICATIONS OF REFRACTION OF LIGHT

Real Depth and Apparent Depth

• An object placed in a denser medium when viewed from a rarer medium appears to be at a depth less than its real depth. This is because of the refraction of light.

• When an object is placed in a rarer medium (like air) and is viewed from a denser medium (like water or glass), it appears to be at a greater distance (or deeper) than its actual position due to refraction of light.

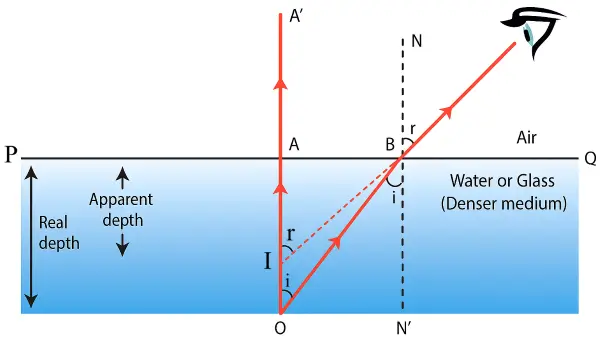
• Real depth, OA : The actual depth at which object is situated is called real depth. 

• Apparent depth, IA : The depth at which image of the object is formed is called apparent depth.

• Shift, OI : Depth by which the object appears to be raised.

Refractive Index, \({{}_a\mu}_m=\frac{Real\;depth}{Apparent\;depth}\)

\(Apparent\;depth\;=\;\frac{Real\;depth}{{{}_a\mu}_m}\)

\(Real\;depth={{}_a\mu}_m\;\times\;Apparent\;depth\)

Shift = real depth – apparent depth

\(Shift\;=\;real\;depth\;\times\left(1-\frac1{{{}_a\mu}_m}\right)\)

Shift depends on:

(i) The refractive index of the medium : Higher the refractive index of the medium, more is the shift.

(ii) The thickness of the denser medium : Thicker the medium, more is the shift.

(iii) The colour or wavelength of incident light : The shift decreases with the increase in the wavelength of light used. Shift is maximum for violet light and minimum for red light.

\(Shift\;\propto Refractive\;Index\;(\mu)\;\propto\;\frac1{wavelength\;\;of\;\;light\;(\lambda)}\)

Consequences  of  Refraction  of  Light

• Stick or pencil bend and shorten when immersed in water.

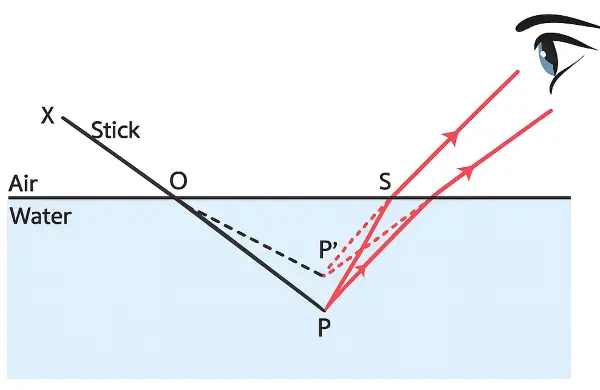
• A star appears to twinkle in the sky. Stars twinkle on account of atmospheric refraction. Starlight undergoes refraction many times before reaching the Earth.

• The apparent position of the star differs from the actual position due to refraction.

• The Sun is seen a few minutes before it rises above the horizon in the morning and a few minutes longer after it sets in the evening.

• A coin kept in a vessel and not visible when seen from just below the edge of the vessel can be viewed from the same position when water is poured into the vessel.

• A print appears to be raised when a glass block is placed over it.
• A tank appears shallow than its actual depth.

SECTION D : CRITICAL ANGLE AND TOTAL INTERNAL REFLECTION

Transmission of Light from a Denser medium to Rarer medium

Case 1 : When  i < C (small angle)

• angle i < angle r
• angle i < angle C
• Both refraction and weak reflection occur.

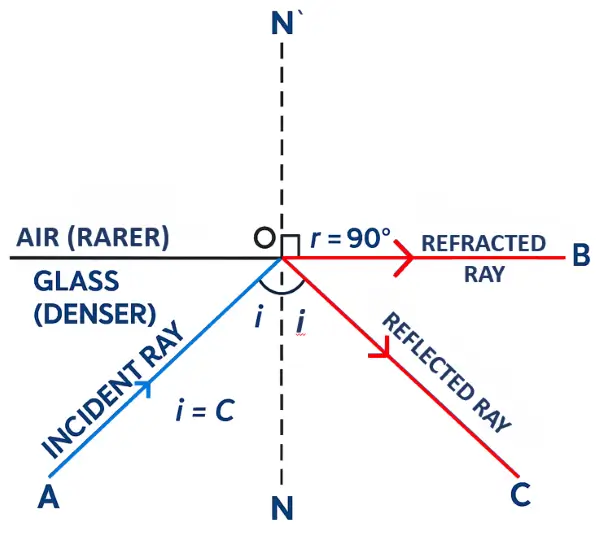
Case 2 : When i = C (critical angle)

• angle i < angle r
• angle i = C
• angle r = 90°
• Refracted ray travels along the surface

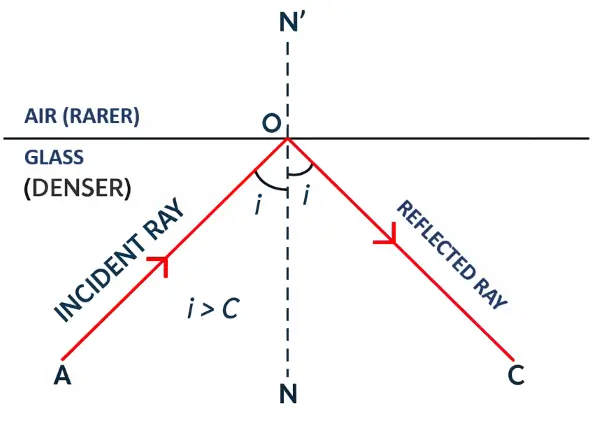
Case 3 : When i > C (greater angle)

• Total internal reflection occurs
• No refraction

CRITICAL ANGLE

When the light ray is travelling from denser to rarer medium such that the angle of refraction in the rarer medium is 90°, then the angle of incidence in the denser medium is called critical angle.

***Note

Critical angle for diamond is 24°, means that, when light travels from the diamond to air, the angle of incident is 24° for which the angle of refraction will be 90°.

RELATIONSHIP  BETWEEN  CRITICAL  ANGLE AND RETRACTIVE INDEX

\({{}_a\mu}_g=\frac1{\sin\;C}\)

\(\sin\;C=\frac1{{{}_a\mu}_g}\)

Factors affecting the critical angle

The critical angle depends on two factors:

(i) The colour or wavelength of light : The critical angle for a pair of media is least for the violet light and most for the red light. Thus the critical angle increases with the increase in wavelength of light.

(ii) The temperature : On increasing the temperature of medium, its refractive index decreases. So, the critical angle increases with increase in temperature.

Total Internal Reflection

When a ray of light travels from a denser to a rarer medium with an angle of incidence greater than critical angle, then no refraction takes place and the entire light is reflected back in the denser medium obeying the laws of reflection. This is known as total internal reflection.

***Note: In the process of total internal reflection, 100% of energy (or intensity) of light is reflected back.

Conditions for total internal reflection

The two necessary conditions for total internal reflection are —

(i) The light must travel from a denser medium to a rarer medium.

(ii) The angle of incidence must be greater than the critical angle for the pair of media.

Total  Internal  Reflection  in  a  Prism 

Total internal reflection in three different prisms :

1. Right angled isosceles prism or total reflecting prism (45°, 90°, 45°)
2. Equilateral triangle (each angle 60°)
3. Right angled prism (30°, 90°, 60°)

1. Right angled isosceles prism or total reflecting prism (45°, 90°, 45°)

Total reflecting prism :  A prism with an angle of 90° between its two refracting surfaces and the other two angles each equal to 45° is called a total reflecting prism because the light incident normally on any of its faces suffers total internal reflection inside the prism. 

The use of total reflecting prism give us an image much brighter than that obtained by using plane mirror.

This prism is used for the following three purposes: 

(i) To deviate a ray of light through 90°

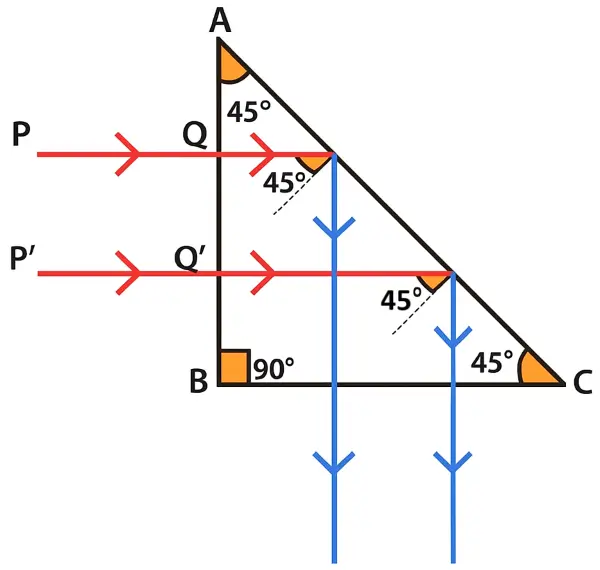
• \(\angle i=45°\)
•  \(\angle i_c=42°\) (Say)
• Light enters normally at face AB → No deviation (No Refraction)

• Hits face AC at 45° (i > critical angle)  → Total Internal Reflection (TIR) occurs.

• Ray is reflected at 90° from the original path.

Used in: Periscopes

(ii) To deviate a ray of light through 180°

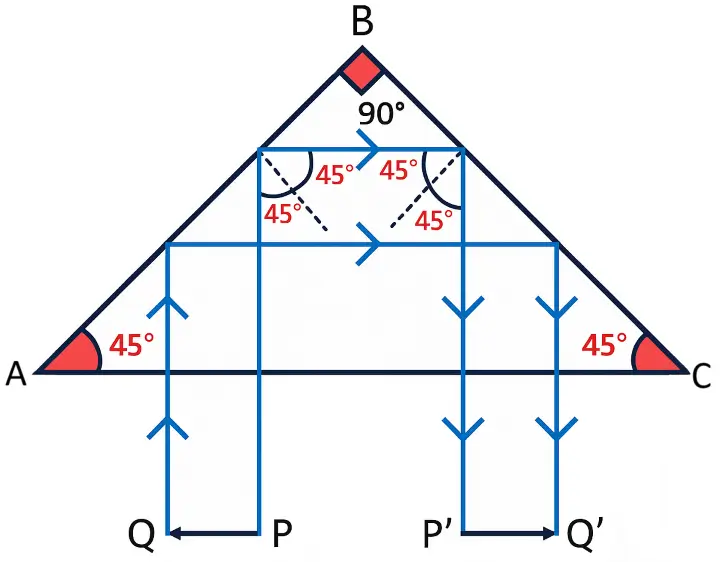
• \(\angle i=45°\)
•  \(\angle i_c=42°\) (Say)
• Light enters normally on face AC.
• Two TIRs occur: first at AB, then at BC (both 45°)
• Emerges opposite to incident direction.
• Total deviation = 180°
• No refraction, No Deviation occurs

Used in: Binoculars, cameras.

(iii) To erect an inverted image without deviation (Erecting prism)

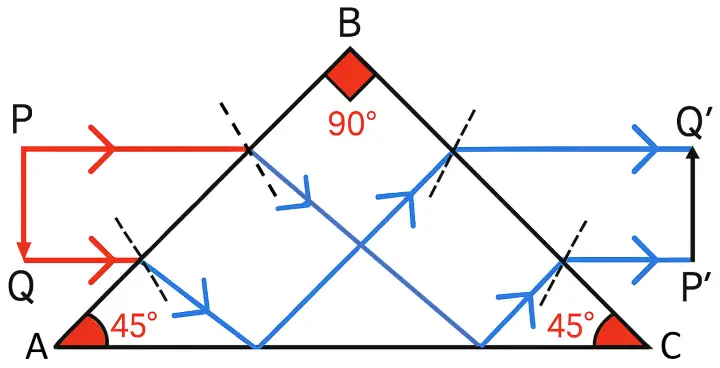
• Light enters parallel to face AC.
• TIR at face AB, then refracted at face AC.
• The face AC behaves like a mirror due to TIR.
• No deviation in direction, but inverted image becomes erect.

Used in: Slide projectors.

2. Equilateral triangle (each angle 60°)

• \(\angle i=45°\)
•  \(\angle i_c=42°\) (Say)
• TIR takes place, No refraction
• Prism ABC, all angles = 60°.
• Light incident normally on face AB → passes undeviated.
• Strikes face AC at 60° → TIR occurs.
• Then strikes face BC at 60° → TIR occurs again.
• Emerges undeviated → net deviation = 60°.

3. Right angled prism (30°, 90°, 60°)

(i) Incident normally on face BC  (side opposite to 30°)

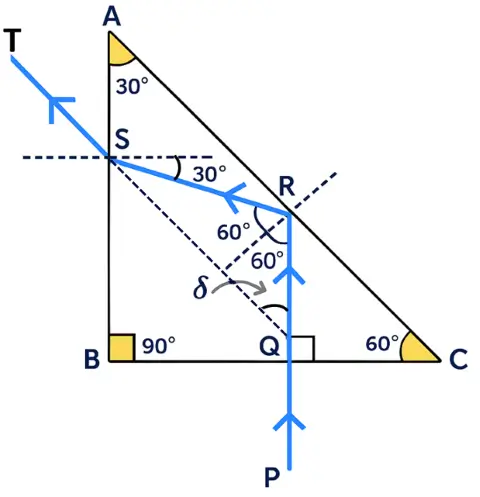
• At face AC: TIR because (\angle i=60° (i>c)\); light ray passing from Denser to rarer medium
• At face BC: No deviation
• At face AB: No TIR  because \(i < c\); only refraction;
  \(\angle i=30°\) and \(c=42°\)

(ii) Incident normally on face AB  (side opposite to 60°)

• Condition: Light ray incident normally on face AB of the prism.

• Result: No total internal reflection.

• Reason: The angle of incidence inside the prism is 30°, which is less than the critical angle (42°).
• Outcome: Light ray gets refracted, not reflected.

(iii) Incident  normally on face AC (side opposite to 90°)

• Condition: Light incident normally on the hypotenuse face (AC) below the foot of the perpendicular from the opposite corner.

• Result: Total internal reflection takes place.

• Outcome: Ray gets deviated by an angle > 60°.

Difference between Reflection from a plane mirror and Total internal reflection

Reflection from a plane mirror	Total internal Reflection
It occurs when light is incident on a plane mirror from any medium at any angle of incidence.	It occurs when light passes from a denser medium to a rarer medium at an angle of incidence greater than the critical angle for that pair of media.
Only a part of light is reflected while the rest is refracted and absorbed.	The entire light is reflected.
There is a loss of energy. The energy of the reflected light is less than that of the incident light.	There is no loss of energy. The  energy of the reflected light is the same as that of the incident light.
The image is less bright and the brightness gradually decreases as silvering on mirror becomes old and rough.	The image is much brighter and the brightness is permanent.

Consequences of Total Internal Reflection 

• Mirage: Illusion of water on hot roads/deserts.

• Test tube in water: Shines like a mirror at certain angles.

• Cracks in glass: Shine due to internal reflection.

• Diamond sparkle: Caused by multiple TIRs inside the gem.

• Optical fibers: Use TIR to transmit light over long distances with minimal loss.

ICSE Class 10 Physics Notes PDF – Refraction of Light at Plane Surfaces

Download free ICSE Class 10 Physics notes on Refraction of Light at Plane Surfaces in PDF format. Includes formulas, solved numericals, and Selina textbook solutions for quick exam revision.

Exam Preparation Tips

• Memorize laws of refraction and key formulas.
• Practice Selina ICSE Physics Chapter 4 solved examples as similar questions often appear in board exams.
• Understand real-life examples of refraction like a straw appearing bent in water, or a coin seeming closer than it is.

You can also visit :

ICSE Class 10 Physics

ICSE Class 10 Chemistry

ICSE Class 10 Mathematics

ICSE Class 10 Physics Notes

• ICSE Class 10 Physics Chapter 1 – Force Notes

• ICSE Class 10 Physics Chapter 2 – Work, Energy and Power Notes

• ICSE Class 10 Physics Chapter 3 – Machines Notes

• ICSE Class 10 Physics Chapter 4 – Refraction of Light at Plane Surfaces Notes

• ICSE Class 10 Physics Chapter 5 – Refraction through Lens Notes Notes

• ICSE Class 10 Physics Chapter 6 – Refraction through Lens Notes

• ICSE Class 10 Physics Chapter 7 – Spectrum Notes

• ICSE Class 10 Physics Chapter 8 – Current Electricity Notes

• ICSE Class 10 Physics Chapter 9 – Electrical Power and Household Circuits Notes

• ICSE Class 10 Physics Chapter 10 – Electro-magnetism Notes

• ICSE Class 10 Physics Chapter 11 – Calorimetry Notes

• ICSE Class 10 Physics Chapter 12 – Radioactivity  Notes

Official Websites

• Council for the Indian School Certificate Examinations (CISCE)